Klein Bottle
- Lepakshi Ramkiran

- Aug 11, 2020
- 2 min read
Yes! Klein Bottle is a 3-D object with zero volume zero edges, one sided, boundary free object. But, you might say, you can store fluid in it. For that here's why you can, Topologically it has zero volume and Klein Bottle does not have an edge. It's boundary-free, and an ant can walk along the entire surface without ever crossing an edge. And so, a Klein Bottle is one-sided.
A Klein Bottle has one hole. This, in turn, causes it to have one handle. The genus number of an object is the number of holes. Other genus-1 objects include innertubes, bagels, wedding rings, and teacups. A wine bottle has no holes and so is genus 0.
Polynomial equation for a Klein bottle.
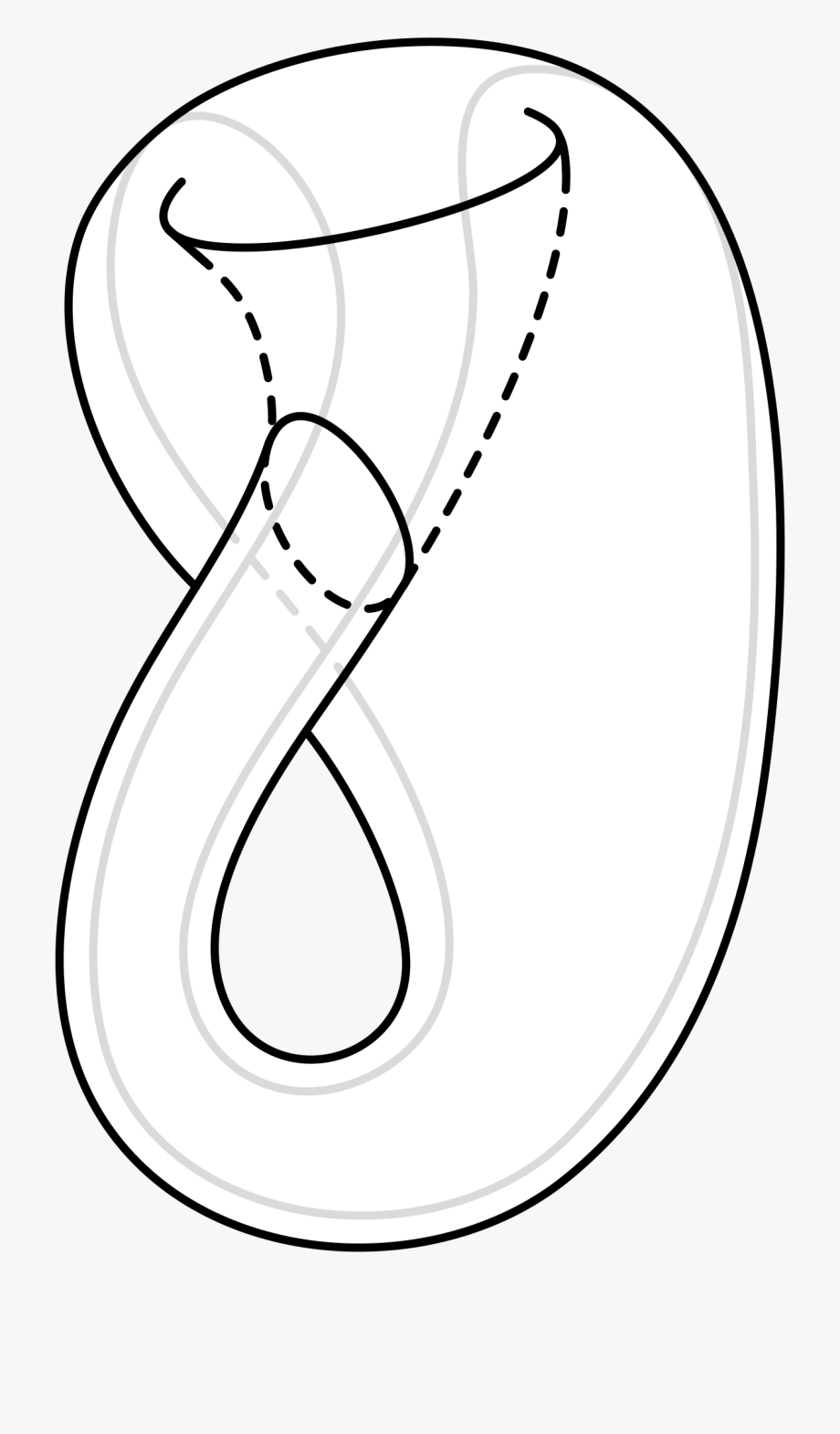
A true Klein Bottle lives in 4-dimensions. But every tiny patch of the Klein Bottle is 2-dimensional. In this sense, a Klein Bottle is a 2-dimensional manifold which can only exist in 4-dimensions!
What we ware seeing is a 3-D immersion of 4-D object). In 4D the Klein bottle doesn't intersect.
For a better analogy assume a sphere and now pass a plane through it. To a 2-D person on the plane the sphere appears to be a circle with it's radius changing and the circle hovering in mid air at places other than the diameter.
Here's a different example: Assume a mobius strip, in 2D it appears to be intersecting as shown below but in 3D it doesn't.
How do you make a Klein bottle?
Take a right handed mobius strip and a left handed mobius strip and join the edge voila we have a Klein Bottle. This will be difficult if you try with paper. Try Knitting it, it would be bit better.
Or if you are are too lazy then you can buy one made of Glass!!
The person who makes the Klein Bottles is the one who inspired me to learn more about Topology. This article is just a scratch about Klein Bottles. All the above mentioned stuff is what I learnt inspired from
His name is Cliff Stoll.
To buy the bottles visit here:
Watch the following fascinating playlist about Klein Bottles.
Credits: Numberphile and Cliff Stoll






Comments