Why square of π is approximately equal to acceleration due to gravity of Earth.
- Lepakshi Ramkiran

- Jul 20, 2020
- 2 min read

π is a wonderful number. It pops up in all sorts of different unexpected places.
But have you ever made a connection between g and π. If so have you thought why square of π is approximately equal to g.
Here's why.
The following proof was proposed by John Wilkins who was an Anglican clergyman, natural philosopher and author, and was one of the founders of the Royal Society.
Getting to the proof, we need to understand how we derive time period of the pendulum.
Simple pendulums are sometimes used as an example of simple harmonic motion, since their motion is periodic. They also fit the criteria that the bob's velocity is maximum as it passes through equilibrium and its acceleration is minimal while at each endpoint. But a deeper understanding of the behavior of the bob will show us that pendulums do not truly fit the SHM model.
To begin our analysis, we will start with a study of the properties of force and acceleration in a simple pendulum by examining a free body diagram of a pendulum bob.

As the pendulum swings, it is accelerating both centripetally, towards the point of suspension and tangentially, towards its equilibrium position. It is its linear, tangential acceleration that connects a pendulum with simple harmonic motion.
The weight component, mg sinθ, is accelerating the mass towards equilibrium along the arc of the circle. This component is called the restoring force of the pendulum.
Restoring Force = mass times tangential acceleration mg sinθ = mass times tangential acceleration
To strictly qualify as SHM this restoring force should be directly proportional to the bob’s linear displacement from equilibrium along the length of the chord.
Geometrically, the arc length, s, is directly proportional to the magnitude of the central angle, θ, according to the formula s = rθ. In our diagram the radius of the circle, r, is equal to L, the length of the pendulum. Thus, s = Lθ, where θ must be measured in radians. Substituting into the equation for SHM, we get:
Restoring Force = - ks
mg sinθ = - k(Lθ)
Solving for the "spring constant" or k for a pendulum yields
mg sinθ = k(Lθ)
k = mg sinθ / Lθ
When an angle is expressed in radians, mathematicians generally represent the angle with the variable x instead of θ. Note that the value of sin x approximates the value of x for small angles; that is,
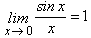
Or, equivalently, for x equal to small values you can see from this power series that the value of sin x would approach that of x.
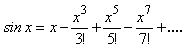
Using this relationship allows us to reduce our expression for the pendulum's "spring constant" to
k = mg / L
Substituting this value for k into the SHM equation for the period of an oscillating system results in
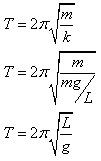
Now we have the Formula for Time period lets substitute known values into it.
then we get squared of π is equal to acceleration due to gravity g.






Comments